Подробное руководство: как найти тангенс смежного угла методом разложения на простые множители

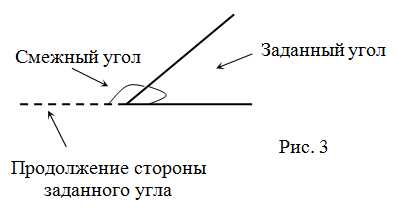
Сравнительно немногие люди овладели техниками вычисления тангенса смежного угла. Это сложный, но возможный для понимания математический концепт, который требует знания углов и основ тригонометрии. В этом руководстве я хочу провести тебя через эти сложные сведения и показать, как шаг за шагом найти тангенс смежного угла. Помните, каждый угол и каждый смежный угол уникален, и нужно узнать, как обрабатывать каждую отдельную ситуацию. Так что давайте начнем наше путешествие в мир сложных, но интересных тригонометрических уравнений и функций!

Смежные углы в тригонометрии: найдем их тангенс!

Начнем с основ. Смежные углы – это такие углы, которые имеют общую вершину и одну общую сторону, а вторые их стороны образуют прямую линию. Проще говоря, два угла считаются смежными, если сумма их мер равна 180 градусам. Звучит довольно интересно, а?

Но что же такое тангенс смежного угла в тригонометрии?

С точки зрения тригонометрии, тангенс угла – это отношение синуса этого угла к его косинусу. А смежный угол – этот угол плюс 180 градусов. Так что, по сути, чтобы найти тангенс смежного угла, нам нужно просто найти тангенс нашего угла, а затем применить формулу добавления углов. Просто как 1-2-3, правда? Не так страшно, как казалось на первый взгляд, правда?

Но есть кое-что, что стоит упомянуть об этом процессе.

• Тригонометрия — это точная наука, поэтому нужно быть точным в своих вычислениях. Никаких округлений «до ближайшего» здесь просто нет!
• Помните, что рабочие углы в тригонометрии задаются в радианах, а не в градусах. Это всегда важно при переводе углов и работы со значениями. Тот важный момент, который не стоит упускать из виду.

Хорошо, мы разобрались с понятием смежных углов и тангенса смежного угла. Но давай честно, у вас есть любимые темы в тригонометрии? Как бы вы оценили свои навыки в этой области на шкале от 1 до 10? С тригонометрией у вас всегда будет возможность узнать больше, и это то, что делает ее такой захватывающей!

Определение и характеристика смежных углов

Смежные углы по праву занимают важное место в науке о геометрии. Что это такое? Такие углы, которые соседствуют друг с другом и образуют совместную сторону. Стойте обратите внимание на это: их общая вершина располагается на одной и той же прямой, что и отмеченные стороны получившихся углов.

Например, углы AOВ и ВОС являются смежными. Когда они соседствуют, у них одна общая сторона — ОВ, и они лежат по обеим сторонам от неё. Заметили? Дальше еще интереснее!

Может быть и так, что совместная сторона углов будет содержать половину окружности. В этом случае сумма углов равна 180 градусов.

Важные характеристики смежных углов

• Смежные углы имеют общую вершину и сторону.
• Сумма смежных углов всегда равна 180 градусам.
• Смежные углы не пересекаются.

Каждый придуманый угол может иметь своего смежника, важно что бы это было действительно выполнение всех условий. Верно, читатель?

Смежные углы могут быть острыми, тупыми или прямыми.

Тангенс в тригонометрии: что это такое?

Вам когда-нибудь понадобилось найти тангенс смежного угла, и вы не были уверены, как это делается? Или вы знали, но были в замешательстве от всех этих синусов, косинусов, тангенсов и так далее? Не бойтесь, кто-то другой тоже это проходил! Но сегодня мы научим вас легко решать эту проблему. Значит, нам нужно разобраться, что такое этот тангенс?

Тангенс – это одна из основных тригонометрических функций, часто упоминаемая наряду с синусом и косинусом. Может показаться, что это что-то такое сложное и непонятное, но на самом деле все довольно прямолинейно. Все эти термины – синус, косинус и тангенс – могут быть вычислены с помощью простой геометрии. Если вы абсолютно новичок в этом, ничего страшного. Точно знаете, что вы уже слышали об этом в школе и просто забыли. Помните, что тангенс угла в правильном треугольнике – это просто отношение противоположного катета к прилежащему. Вы когда-нибудь задумывались об этом? Это просто отношение длины двух линий друг к другу. Ничего сложного!

А знаете ли вы, что тангенс невозможно найти для каждого угла? Например, для угла в 90 и 270 градусов! Что может быть удивительней? Вы ведь скажете: «Но ведь угол в 90 градусов, это же вертикальная линия. Как это — нет тангенса?». А спросите, где при этом прилежащий катет? Ну вот, и получается, что для таких углов тангенса нет.

В общем, каждый раз, когда вы сталкиваетесь с задачей по тригонометрии, помните о том, что тангенс – это просто отношение длин сторон треугольника, и ключевой перспективой является одно: практика. Как говорится, практика делает мастера. Просто попрактикуйтесь в расчётах, отрепетируйте их несколько раз, и всё будет выглядеть проще. Удачи в понимании и применении всех ваших тригонометрических функций!

Об удивительном свойстве тангенса и его вычислении

Вы не чувствуете себя вдохновленным? Это же просто математика! Но подожди, тут главное уловить суть. Ведь все гениальное просто, не так ли?

Математическая сущность тангенса и его формула

Нет ничего проще и яснее, чем формула нашего дорогого тангенса:

tg(α) = sin(α)/cos(α)

Вам видно, да? Суть тангенса для любого угла α: это просто отношение синуса угла к его косинусу!

Говоря простыми словами, вот как вы это вычисляете:

1. Сначала найдите значение синуса для вашего угла (не волнуйтесь, калькуляторы сегодня могут это легко сделать).
2. Затем вычислите косинус того же угла.
3. Наконец, чтобы получить тангенс, просто поделите результат первого шага на результат второго.

Вот и все, в принципе. Тангенс – это лишь отношение синуса угла к его косинусу. Возможно, сначала это покажется вам сложным, но представьте себе, что это так просто, как открыть дверь или заварить чашку кофе. Математика позволяет нам открывать новые двери в нашем понимании мира. Так что вы готовы войти?

Находим тангенс смежного угла: наглядно и доступно!

Возникало ли у вас такое, что упорно пытаешься найти тангенс угла, и никак не получается? И вот смотришь на этот угол, сколько-то там градусов, и думаешь: «Так, стоп. Тангенс. Это же как?». Признаюсь, и у меня такое было. Но знаете что? Я научился этому! И потому с уверенностью могу сказать: такое же можно добиться и вами. Готовы? Поехали!

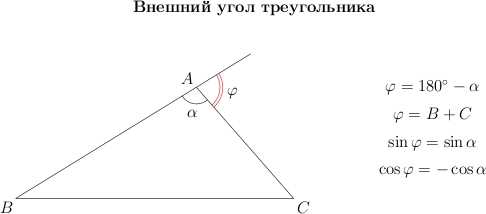
Представим, что у нас есть угол A. Его смежным будет угол, который вместе с ним образует прямую линию или, иначе говоря, 180 градусов. Пускай это будет угол B. Получается такая вот штука — если угол A составляет, например, 60 градусов, то угол B будет равен 120 градусов. А все потому, что 180-60=120. Просто математика. Что ж, каким будет тангенс этого смежного угла?

Не так сложно, как кажется!

Я согласен, глядя на это всё сначала, может показаться, что это какая-то ракетная наука. Но это вовсе не так! Здесь все довольно просто. Итак, математически тангенс смежного угла определяется как тангенс исходного угла минус 180 градусов, то есть tg(180 — a). Но стоп, не так все просто. Ведь тангенс угла в 180 градусов не определён. Так как же быть?

Правило жизни: есть исключения из правил.

И вот тут на помощь приходит одно неплохое правило, которым я пользоватся всегда. Помните, я сказал, что раз пришло время математики? Так вот, математически всегда верно, что тангенс угла, дополняющего до 180 градусов, равен тангенсу исходного угла, то есть tg(a) = tg(180 — a). Но лишь в том случае, когда a находится в интервале от 0 до 90 градусов. Запомнили? Только от 0 до 90. Это очень важно. С этим надумать ошибиться просто невозможно.

А как быть с углами более 90 градусов?

Об этом тоже думали математики. Если угол больше 90 градусов, то тангенс смежного угла будет равен тангенсу 180 минус этот угол. То есть, для нашего случая с углом в 120 градусов это будет tg(180 — 120) = tg(60). Получается просто. Тангенс 60 градусов, это ведь уже не страшный зверь, верно? Здорово получается, правда?

Учиться получается гораздо легче, когда вместе, правда? Именно об этом и есть вся математика — про учиться вместе, про преодолевать сложное вместе, про находить ответы на вопросы вместе. Верю в вас, вы справитесь!

Последний штрих: тангенс равен синусу делить на косинус.

И последнее, что стоит запомнить, это то, что тангенс угла равен отношению синуса этого угла к его косинусу. Именно так, синус делить на косинус. Не наоборот! Теперь вы готовы решить любую задачу с тангенсами. Умница! Вперед, навстречу новым знаниям!

Расчет тангенса смежного угла

Тут важно помнить формулу tg(180-a) = -tg(a), где a — наш изначальный угол, а 180 — уже смежный угол. Как мы видим, тригонометрия это вовсе не чёрная магия. Верно?

Давайте проработаем эту формулу на примере. Возьмем угол в 30 градусов. Вы уже знаете что tg(30) примерно равен 0.577, так?

• По формуле, которую мы упомянули ранее, tg(180-30) = -tg(30), мы получим значение тангенса для смежного угла. Вычислим?
• Заменяя наши значения в формуле, получим: tg(150) = -0.577. Вот и всё, ничего сложного, правильно?

Напомню, что в случае тригонометрии, ключевым является понимание формул и логики их работы. Можете использовать этот подход для любых углов. Видите, как всё упрощается, когда знаешь основы?

Так что ж, что мы имеем в итоге? С помощью одной простой формулы мы преодолели гору сомнений и сложностей, нашли тангенс смежного угла и открыли себе новые возможности! Как по мне, эта вещь великолепна. А вы что думаете?

Проколы при вычислении тангенса смежного угла

Ой, да было дело, даже самые умные молодцы случайно используют не те формулы. Иногда, мозг так сказать скользит по старым дорожкам, и вместо того, чтобы использовать tg (180 — α) = -tg α или tg (180 + α) = -tg α, ошибочно применяют формулы для синуса или косинуса. Итог? Углы, которые как бы и не существуют, получаются.

А что, если смежность углов вы определите неправильно? Представляете? Неверное определение смежного угла может поставить зеркало к углу на 180 градусов. Тут на помощь приходит главное предположение о смежных углах: они всегда дополняют угол до 180 градусов. Раз не так — и дорога в бездну ошибок открыта!

Ошибки в математических операциях

Даже при проведении базовых математических операций ошибки тоже могут встречаться. А какие ещё бывают ошибки? Кто-нибудь забывает ли делить на ноль? Кто-нибудь запутывает цифры? Всё бывает, и верно?

• Ошибки в сложении и вычитании. Недосчитать или, наоборот, пересчитать — это что-то, что нам всем знакомо.
• Умножение или деление на ноль. Берегите себя от этого! Это арифметическая смертная казнь.
• Отсутствие контрольной проверки. Никогда не забывайте ее делать, иначе рискуете запутаться в мнимых решениях.

В общем, главное, не унывать. Даже самые умные люди часто ошибаются. Независимо от транжира или списка проколов, главное в обучении — это кепка. Ну и, конечно же, понимание.

Анализ типичных проблем и практические советы по их избежанию

При поиске тангенса смежного угла студенты часто сталкиваются с проблемами и общими ошибками. Ниже мы проанализируем некоторые из наиболее распространенных трудностей и предложим практические советы по их предотвращению.

Разберемся, как можно эффективно научиться находить тангенс смежного угла, минимизируя возможные ошибки в расчетах.

Типичные проблемы и советы по их избежанию

1. Трудности с пониманием того, что такое смежный угол.Совет: Убедитесь, что вы точно понимаете, что такое смежные углы. Это два угла, у которых общая сторона и общая вершина, однако они не имеют общих внутренних точек.
2. Ошибка в использовании формулы тангенса.Совет: Всегда проверяйте, правильно ли вы используете формулу. Тангенс угла равен синусу этого угла, деленному на его косинус.
3. Заблуждения связанные с тем, что смежные углы равны.Совет: Смежные углы не всегда равны. Их сумма равна 180 градусам, но каждый угол может быть любым числом до 180.

Помимо этих типичных ошибок, общим советом является практика и постоянное использование ваших знаний на практике. Чем больше вы взаимодействуете с математическими формулами и концепциями, тем проще становятся задачи, в которых они применяются.