В жизни каждого студента есть момент, когда он сталкивается с задачей нахождения наименьшего и наибольшего значения алгебраического выражения. Это может показаться сложным, но не стоит отчаиваться. Существуют простые и эффективные методы и способы, которые помогут вам быстро и без проблем найти искомые значения. Это не только облегчит выполнение вашего домашнего задания, но и поможет развить логическое мышление, что пригодится в будущем. Давайте окунёмся в это увлекательное путешествие по математике, и я поделюсь с вами некоторыми проверенными советами и способами решения подобных задач.
- Зачем нужно уметь находить минимум и максимум выражений
- Практическое применение навыка нахождения крайних значений
- Устные способы решения
- Создайте визуальное представление
- Похождение за минимумом и максимумом с помощью логики и арифметики
- Логический подход: где найти минимум и максимум?
- Арифметика в действии: разложение на множители
- Письменные методы поиска крайних значений
- Метод Дифференцирования
- Метод второго дифференциала
- Алгебраические методы решения задачи о нахождении наименьшего и наибольшего значения выражения
- Советы и шаги: на пути к пониманию
- Использование дифференциального исчисления для нахождения максимума и минимума функции
- Заключение: значение производной в поиске экстремумов функции
- Полезные советы и способы
Зачем нужно уметь находить минимум и максимум выражений
Такой спутник, как математика, помогает нам во многих областях жизни. Вы когда-нибудь задумывались, как ключевую роль играет умение находить минимум и максимум выражений?
Они знают, где скрываются секреты оптимизации. Говоря проще, они помогут вам выжать максимум из ситуации или избежать максимальных потерь.
Есть много причин, по которым это жизненно необходимый навык:
- В бизнесе вы хотите направить свои ресурсы наиболее эффективным образом. Где лучше инвестировать? Куда направить рекламу? Как выполнять работу быстрее? Все эти вопросы требуют поиска максимального и минимального значения.
- В повседневной жизни тоже нужен поиск экстремумов. Допустим, вы ездите на работу и хотите минимизировать время поездки — ищете минимум. Или пытаетесь найти самую качественную еду по минимальной цене — опять минимум.
- В научных исследованиях также не обойтись без этого навыка. Решение большинства задач связано с определением максимума или минимума функций.
Вы поймете, что уметь находить минимум и максимум выражений – это как владеть навигатором в мире решений. Готовы ли вы повысить свой навык в этом?
Экстремумы вокруг нас! Работа с ними способствует точности, оптимизации и, в конечном итоге, успеху. Какой первый шаг вы сделаете для того, чтобы научиться этому?
Практическое применение навыка нахождения крайних значений
И еще одно. Мало кто задумывается, но навык нахождения наибольшего или наименьшего значения выражения жизненно важен для таких профессий, как инженеры, бизнес-аналитики, экономисты или математики. Задумались почему? Например, экономисту нужно уметь оптимизировать бюджет, чтобы при максимальных доходах минимизировать расходы. Именно такой навык позволит выжить малому бизнесу в жесткой экономической ситуации.
Как вы думаете, насколько важно уметь находить крайние значения в повседневной жизни? Способны ли вы применить эти знания на практике?
Это не просто понимание, сколько стоит килограмм яблок или литр бензина. Это навык, который помогает вам лучше понимать окружающую реальность, принимать правильные и взвешенные решения, и в результате — просто жить лучше.
- Определите цель. За что вы хотите получить максимум или минимум?
- Определите переменные. Какие факторы могут повлиять на результат?
- Постройте модель. Определите математическую функцию, которая описывает вашу задачу.
- Найдите крайние значения. Это поможет вам принимать рациональные решения.
Не стоит забывать: умение находить минимальные и максимальные значения выражения поможет вам не только в делах, связанных с бизнесом или наукой, но и в обычной жизни. Вы ведь хотите получить максимум удовольствия от еды, отдыха, жизни в принципе? Значит, этот навык вам точно не помешает!
Устные способы решения
Давайте начнем c основ и простоты. Но вы заметите, что эти подходы не менее эффективны из-за их простоты. Это то, что делает их такими удивительными.
Создайте визуальное представление
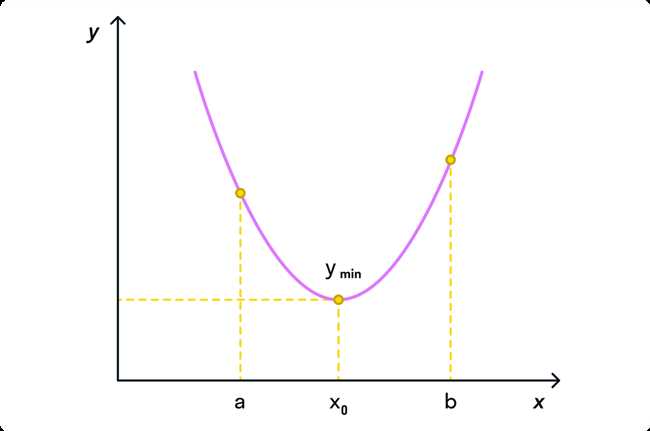
Знаете, как мы люди склонны к визуализации? Мы можем придумать истории и строить картину в нашем уме, чтобы лучше понять то, что происходит. Почему бы этот подход не использовать при нахождении наименьшего и наибольшего значения выражения? Попробуйте чертить графики, если работаете с кривыми, или использовать численные линии при работе с серией чисел. Так вам проще будет увидеть, где находятся эти значения.
Так что, мы делаем? Берем карандаш и листик бумаги и начинаем строить и раскрашивать нашу диаграмму? Вовсе нет. Все это в нашем уме. Помогает? В целом — да, согласны.
Вы думаете, что это звучит невероятно? Соглашаюсь, но вот интересное — этот подход работает. У нас есть способность создавать картинки в уме. Почему бы не использовать ее для упрощения нашей задачи?
Но как быть, если мы действительно запутались? Бывает и такое, верно? И с этим мы тоже можем справиться.
- Попробуйте сначала решить задачу в уме. Не надо отчаиваться, если не получается.
- Следующий шаг — выйти на воздух, прогуляться, отдохнуть. Вернитесь к задаче с новыми силами.
- Если же все еще слишком сложно, определите, в чем именно возникли сложности и устраните их. Может быть, стоит еще раз освежить в памяти теорию? Главное — не втягиваться в спираль отчаяния.
Видишь, на самом деле твой мозг — суперсила. Исключительно сильный инструмент, благодаря которому ты можешь сделать многое. Просто поверь в это и попробуй применить свои способности.
Так что наша задача — определить минимальное и максимальное значение выражения — довольно выполнима, если мы применим немного усилий и подключим свою умную голову. Уверен, что у вас все получится.
Похождение за минимумом и максимумом с помощью логики и арифметики
Разумеется, мы сейчас вовсе не будем искать бирюзовые моря или секретные рецепты благополучия, но не менее важным и невероятно интересным будет наш сегодняшний поиск минимума и максимума выражения! Согласны присоединиться?
Логический подход: где найти минимум и максимум?
Зачастую, применяя силу своего критического мышления, можно обнаружить минимальное или максимальное значение выражения. Давайте рассмотрим пример. Вы пытаетесь найти максимум функции x^2 на отрезке от -1 до 1. Согласитесь, что и при x=-1, и при x=1 значение функции будет одно и то же — равное 1. И, более того, вас наверняка убедит тот факт, что при всех других x на этом отрезке значение будет меньше. Очевидно, верно? Ура, вы нашли максимум!
Эй, маэстро арифметики, вы готовы к своему выступлению?
Арифметика в действии: разложение на множители
Если функция выглядит комбинированно, возникает вопрос, как найти её минимум и максимум. Часто эффективным методом является разложение на множители. Представьте, что вы столкнулись с выражением вида (a+b)^2. Вы разложите его на множители и получите a^2+2ab+b^2. А здесь уже можно увидеть, что минимальное значение функции достигается при a=0 и b=0.
Занимательно, как одни и те же уравнения могут преподнести нам уйму открытий и даже… о, я совсем забыл!
- Светоч надежды: производная
- Истина в последней инстанции: точки экстремума
Как ни странно, но путь к нахождению минимума или максимума значений выражения может лежать через определение его производной. Выполнив эту операцию, вы отыскиваете точки, в которых функция меняет свой знак – и эти точки и будут служить требуемыми нами крайними значениями.
Зачерпнули уйму новых идей? Надеюсь, что наша прогулка в мире минимума и максимума была вам полезна. Не переставайте искать новые горизонты знаний!
Письменные методы поиска крайних значений
Найдем наиболее практичные путь, добиться результата в поиске крайних значений! Давайте начнем с основных шагов решения этой головоломки. Ты увидишь, как просто и интересно может быть to построение графика функции и анализ экстремумов.
Зачастую соискателями наименьших и наибольших значений выражений выступают студенты. Помните, как в университете давали задания нахождения экстремумов функции? Давайте обновим в памяти основные принципы.
Метод Дифференцирования
Начнем с дифференцирования. Что нам может помочь в поиске экстремумов функции? Дифференциал функции — звучит сложно, но на самом деле это наш ключ к решению задачи. Найдя производную, определим точки, где она равна нулю или не существует. Это разделяет график на интервалы. Затем проверяем знак производной в каждом интервале. Если она меняет знак с «+» на «-«, мы нашли локальный максимум, а если наоборот, то мы нашли локальный минимум.
| Производная | Максимум или минимум? |
| С «+» на «-« | Максимум |
| С «-» на «+» | Минимум |
Уверен, это ты помнишь! Интересно, количество студентов, вспомнивших про метод дифференцирования, увеличилось после прочтения этого?
Метод второго дифференциала
А вот метод второго дифференциала немного сложнее. Ты готов вспомнить его? Если взять вторую производную и найти ее знак в точке экстремума, то можно определить, является ли точка максимумом или минимумом. Если второй дифференциал больше нуля, то это минимум, а если меньше нуля — то это максимум.
| Второй дифференциал | Максимум или минимум? |
| Больше 0 | Минимум |
| Меньше 0 | Максимум |
Как думаешь, легче ли стало вспомнить метод второго дифференциала, когда мы разбираем его по шагам? Практика — лучший учитель! Попробуй применить это к реальной задаче — и ты сразу увидишь результат. Помни, что у поиска крайних значений есть столько же разнообразия, сколько и у головоломок. Сканируй пространство, использовав письменные способы, и найди свой путь к решению!
Алгебраические методы решения задачи о нахождении наименьшего и наибольшего значения выражения
Итак, столкнулись с задачей по алгебре, которая заставляет вас подумать: как найти наименьшее или наибольшее значение выражения? Не все так сложно, как леденящий душу термин «алгебраический метод» может заставить вас подумать!
Алгебраический метод по сути — это следование определенному набору математических правил и процедур, чтобы решить задачу. Это довольно системный подход, который, хотя и может показаться сложным, на самом деле делает процесс решения более структурированным и предсказуемым. Так что давайте смело идти вперед!
Производная как инструмент определения экстремумов
Один из самых важных инструментов в алгебраическом подходе — это производная. Понимаете что это такое? Когда мы столкнулись с функцией и хотим найти ее наименьшее или наибольшее значение, мы можем определить где функция достигает своих экстремумов, искользуя производные.
Решение квадратных уравнений: олдскульный подход
Но что если у нас есть квадратное выражение, или, скажем, полиномиальное? В этом случае, метод решения квадратного уравнения — ваш лучший друг. Помните формулу вычисления корней квадратного уравнения? (б-бойтесь… это -b±√(b²-4ac)/2a). С ее помощью вы всегда сможете найти точки, где наибольшее или наименьшее значение экстремума достигается.
Советы и шаги: на пути к пониманию
- Подробное изучение: Сначала внимательно изучите выражение. Какой его тип? Полиномиальный? Квадратное выражение? Это влияет на то, какие методы вам стоит использовать.
- Используйте верные методы: Определите, подходит ли использование производных или решение квадратного уравнения для решения вашей задачи. Каждый из этих методов применяется в определенных ситуациях, так что нет единого «правильного» выбора.
- Практикуйтесь: Практика действительно делает нас лучше. Не переживайте, если не получается с первого раза — продолжайте практиковаться, и у вас все получится!
Пренебрегать алгебраическим методом не стоит. Это важный инструмент в вашем математическом арсенале, который поможет вам решить целый ряд задач. Поэтому давайте не бойтесь алгебры! Вместо этого давайте объяснять ее, понимать и использовать для решения сложных проблем.
Использование дифференциального исчисления для нахождения максимума и минимума функции
Так вот, дифференциальное исчисление к вашим услугам. Уже слышали о нём? Если нет, то это отрасль математики, с помощью которой можно находить минимумы и максимумы. Спасёт нас ведь не простая магия, а наука, да?
Суть метода
Простыми словами, мы с вами будем искать те точки на графике функции, где функция «поворачивает» или «останавливается». Можно представить, что вы идете вверх по горе – в какой-то момент вы достигаете вершины и начинаете спускаться вниз. Вершина горы – это максимум функции. Аналогично с долиной и минимумом.
Исследуем производную
Как же нам найти эти самые вершины и долины? Да с помощью производной, друзья мои! Этот шедевр математики позволяет нам вычисленить скорость изменения функции.
- Находим производную нашей функции.
- Решаем уравнение, приравнивая производную к нулю. Получаем критические точки – возможные максимумы и минимумы.
- Находим вторую производную, чтобы понять, где у нас максимум, а где минимум.
А ведь всё же вполне понятно, правда? Используя дифференциальное исчисление, вы сможете найти все максимумы и минимумы, а значит, оценить лучшие и худшие значения выражения. Этакий исследователь всегда найдет то, что ищет!
Готовы окунуться в мир математических приключений? Знания и умение использовать их – ваш ключ к нахождению максимальных и минимальных значений выражения! Первые шаги за вами, а там – глядишь, и до своего первого научного открытия недалеко!
Заключение: значение производной в поиске экстремумов функции
За некоторыми исключениями, для большинства функций данный метод является действительно удобным и практичным инструментом. К тому же, его можно применить даже в случаях, когда функция не имеет аналитического вида, что является большим преимуществом.
Полезные советы и способы
В завершение, хотелось бы подчеркнуть несколько моментов, которые помогут вам эффективно применять вышеописанный метод на практике:
- Проверка условий: перед применением метода необходимо убедиться, что все его условия выполнены. Функция должна быть дифференцируемой в интересующем нас интервале.
- Точная математика: очень важно проводить все расчеты как можно точнее. Ошибки в расчетах могут привести к неправильным результатам.
- Графическая визуализация: построение графика функции и его анализ могут быть полезными не только в процессе вычисления экстремумов, но и для контроля правильности решения.
Желаем вам успехов в нахождении экстремумов функции и их применении в реальной жизни!






