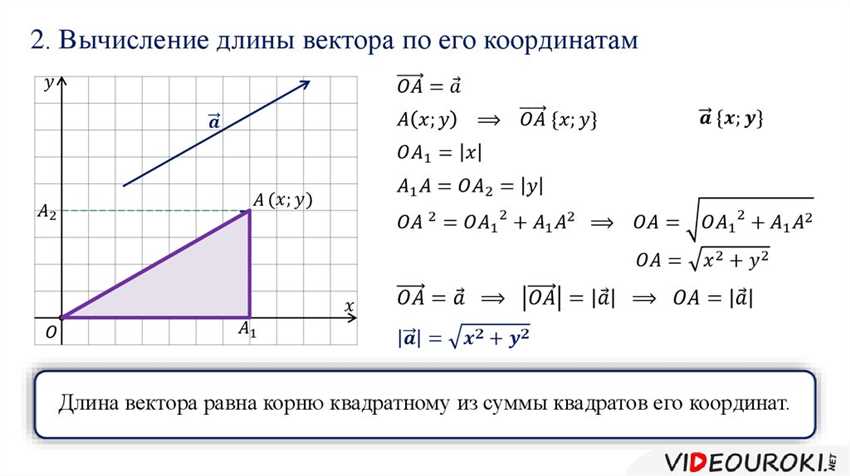
В повседневной жизни мы часто сталкиваемся с понятиями длины, скорости, ускорения и других величин, которые можно представить в виде векторов. Вектор — это направленный отрезок прямой, который имеет длину и направление. Длина вектора — это расстояние от начала вектора до его конца.
Квадрат длины вектора — это величина, которая равна квадрату длины вектора. Квадрат длины вектора часто используется в различных расчетах, например, при определении площади треугольника, площади поверхности многогранника, объема пирамиды и т. д.
В этом статье мы рассмотрим, как рассчитать квадрат длины вектора, а также приведем примеры расчета.
Формула расчета квадрата длины вектора
Формула расчета квадрата длины вектора в прямоугольной системе координат имеет следующий вид:
|a|^2 = a_x^2 + a_y^2 + a_z^2
где:
- |a| — длина вектора
- a_x, a_y, a_z — координаты вектора
В этой формуле квадрат длины вектора равен сумме квадратов координат вектора.
Примеры расчета квадрата длины вектора
Рассмотрим несколько примеров расчета квадрата длины вектора.
Пример 1
Дано вектор a с координатами (2, 3, 4).
|a|^2 = a_x^2 + a_y^2 + a_z^2
|(2, 3, 4)|^2 = 2^2 + 3^2 + 4^2
|a|^2 = 4 + 9 + 16
|a|^2 = 29
Ответ: |a|^2 = 29
Пример 2
Дано вектор b с координатами (-1, 5, -6).
|b|^2 = b_x^2 + b_y^2 + b_z^2
|(-1, 5, -6)|^2 = (-1)^2 + 5^2 + (-6)^2
|b|^2 = 1 + 25 + 36
|b|^2 = 62
Ответ: |b|^2 = 62
Пример 3
Дано вектор c с координатами (0, 0, 0).
|c|^2 = c_x^2 + c_y^2 + c_z^2
|(0, 0, 0)|^2 = (0)^2 + (0)^2 + (0)^2
|c|^2 = 0 + 0 + 0
|c|^2 = 0
Ответ: |c|^2 = 0
Пример 4
Дано вектор d с координатами (1, 2, -3).
|d|^2 = d_x^2 + d_y^2 + d_z^2
|(1, 2, -3)|^2 = 1^2 + 2^2 + (-3)^2
|d|^2 = 1 + 4 + 9
|d|^2 = 14
Ответ: |d|^2 = 14
Пример 5
Дано вектор e с координатами (3, 4, 5).
|e|^2 = e_x^2 + e_y^2 + e_z^2
|(3, 4, 5)|^2 = 3^2 + 4^2 + 5^2
|e|^2 = 9 + 16 + 25
|e|^2 = 50
Ответ: |e|^2 = 50
Пример 6
Дано вектор f с координатами (-2, 3, -4).
|f|^2 = f_x^2 + f_y^2 + f_z^2
|(-2, 3, -4)|^2 = (-2)^2 + 3^2 + (-4)^2
|f|^2 = 4 + 9 + 16
|f|^2 = 30
Ответ: |f|^2 = 30
Пример 7
Дано вектор g с координатами (0, 0, 1).
|g|^2 = g_x^2 + g_y^2 + g_z^2
|(0, 0, 1)|^2 = (0)^2 + (0)^2 + 1^2
|g|^2 = 0 + 0 + 1
|g|^2 = 1
Ответ: |g|^2 = 1
Пример 8
Дано вектор h с координатами (1, 0, 0).
|h|^2 = h_x^2 + h_y^2 + h_z^2
|(1, 0, 0)|^2 = 1^2 + 0^2 + 0^2
|h|^2 = 1 + 0 + 0
|h|^2 = 1
Ответ: |h|^2 = 1
Пример 9
Дано вектор i с координатами (0, 1, 0).
|i|^2 = i_x^2 + i_y^2 + i_z^2
|(0, 1, 0)|^2 = 0^2 + 1^2 + 0^2
|i|^2 = 0 + 1 + 0
|i|^2 = 1
Ответ: |i|^2 = 1
Пример 10
Дано вектор j с координатами (0, 0, 0).
|j|^2 = j_x^2 + j_y^2 + j_z^2
|(0, 0, 0)|^2 = 0^2 + 0^2 + 0^2
|j|^2 = 0 + 0 + 0
|j|^2 = 0
Ответ: |j|^2 = 0
Заключение
Квадрат длины вектора — это величина, которая равна квадрату длины вектора. Квадрат длины вектора часто используется в различных расчетах. Формула расчета квадрата длины вектора в прямоугольной системе координат имеет следующий вид:
|a|^2 = a_x^2 + a_y^2 + a_z^2
где:
|a| — длина вектора
a_x, a_y, a_z — координаты вектора







